How to Figure Out What to Invest Now for a Big, Future Expense

This small house with a trampoline in the backyard looks like my minimalist dream.

All right – before we dive in – let’s get one thing out of the way.

I’m not condoning dropping $100,000 in one fell swoop on pretty much anything. BUT, if for some reason you DO need $100,000 at some future date… I’ll show you how to figure out how much you need to be investing now for it to grow to be worth $100,000 by the time you need it.

Most of the time, the two major examples people love to use this for are (a) buying a home and (b) paying for a kid’s college education.

Please allow me to do my due diligence and get my initial cautionary comments out of the way before we jump into the #formula:

Both of these purchases can be problematic and not great investments: Before you rage-unfollow @moneywithkatie, hear me out. I promise I have your best interests at heart.

If my kid wants to go to UNC Chapel Hill to study elementary education and I’m going to invest $250,000 (minimum) for them to go there without a scholarship in order to get a job making $40,000/year, is that a good investment? Probably not. While it’s great to plan for an expensive-ass college education, remember to use common sense. (As someone without a college-aged kid and barely out of college myself, I feel I am uniquely qualified to make controversial comments on the subject. *winks*)

Just kidding – but you know what I mean! As college educations become more ubiquitous (a college degree is a dime a dozen these days) and wages continue to stagnate, dumping hundreds of thousands of dollars into a college degree isn’t really wise. The scholarship and the in-state schools are your best friends. Hopefully by the time you have a college-aged kid, the bubble will have burst and the cost of college won’t be a quarter of a million dollars anymore, but for the time being, it’s a messed-up system and one in which your ROI is not very good if you pay full price and your kid doesn’t become a doctor, lawyer, or investment banker.

The housing subject is another one entirely – and you’ve probably already seen my hot takes on home ownership. For the purposes of this post, we’re going to assume a few things about your intent to buy a home:

• You’re buying it because you actually want it for your family, and you’re OK if it loses money/isn’t a great investment.

• The down payment you’re saving accounts for 30% or less of your total net worth (the last thing you want to do is spend your entire nest egg on a house – that’s referred to as being “house poor”).

That said, after a certain point, the house can be a good investment – especially if you’re using it as a rental property or you get a really good deal.

My last disclaimer: Because we’re talking about future events, we’re making assumptions that the costs will continue on the same trajectories they’re on today

Just by nature of the fact that we’re figuring out how to pay for a one-time big expense in the future, we’re assuming there won’t be any major changes in (a) what we want and (b) how much it costs.

But alas, we have to plan and make decisions based on the information we have right now. Even if it’s inherently speculative in some ways, the alternative path is not planning at all for anything, and that’s no good. We have to do our best with what we know.

The “present value” formula

The present value formula is your best friend when planning for one-time future expenses, and you can factor this in to your “FI” number by looking at both opportunity cost and how much additional you’ll need to be saving and investing in order to pay for your “thing” in the future.

Ready to have PTSD from physics class? It looks like this:

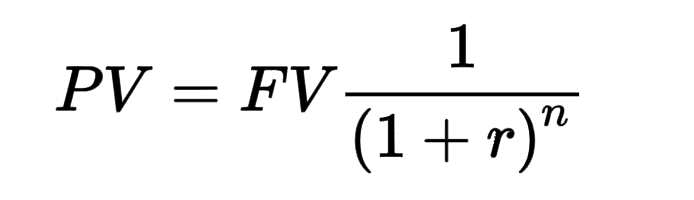
Are you having pain-flashbacks to WebAssign software? Because I am.

Ok. Let’s dumb this down so people who studied public relations in college (read: me) can understand what’s happening here.

PV means you’re solving for the present value of something. That’s what you see on the left side of the equation, which means you’re figuring out what you need to invest today in order for it to grow to the future value (or FV, in the equation) that you want it to be.

The 1 over (1+r)^n is just the chunk that accounts for the fact that your money is compounding. The “r” is the rate you’re expecting to get (7% is the average) and “n” is the number of years between you and the event at hand.

College tuition example

Let’s pretend you plan to have a kid in 5 years. This means your timeline for saving for college is 5 years + 18 years (five years before you have the kid, and then 18 years for them to reach college age).

This means you have 23 years for your money to compound to be worth $250,000 – I’m estimating $62,500/year for college, in this example. I can already see how this is problematic, because this is how much an expensive college costs today – but I don’t think it’ll continue to increase at its current rate (mostly because it just can’t, economically).

Regardless, for the sake of the math, here’s what you’d do:

PV = $250,000 * (1/((1+0.07)^23))

Or, you can remember that you live in 2020, and use this Present Value calculator instead. Remember? PR major.

I plugged in these numbers and found out I’d need to have $52,736 invested today to have $250,000 by the time my hypothetical child I’d have at age 30 turns 18. Candidly, that’s not super helpful to know, so I prefer to use the “periodic deposits” side of the calculator to figure out how much I’d actually have to invest every year in order for it to be worth $250,000 in 23 years.

By doing both, I can see my options: Either sock away $52,000 now and let it grow (if I have it), or (and this is actually quite realistic) invest $4,700 per year for the next 23 years for college.

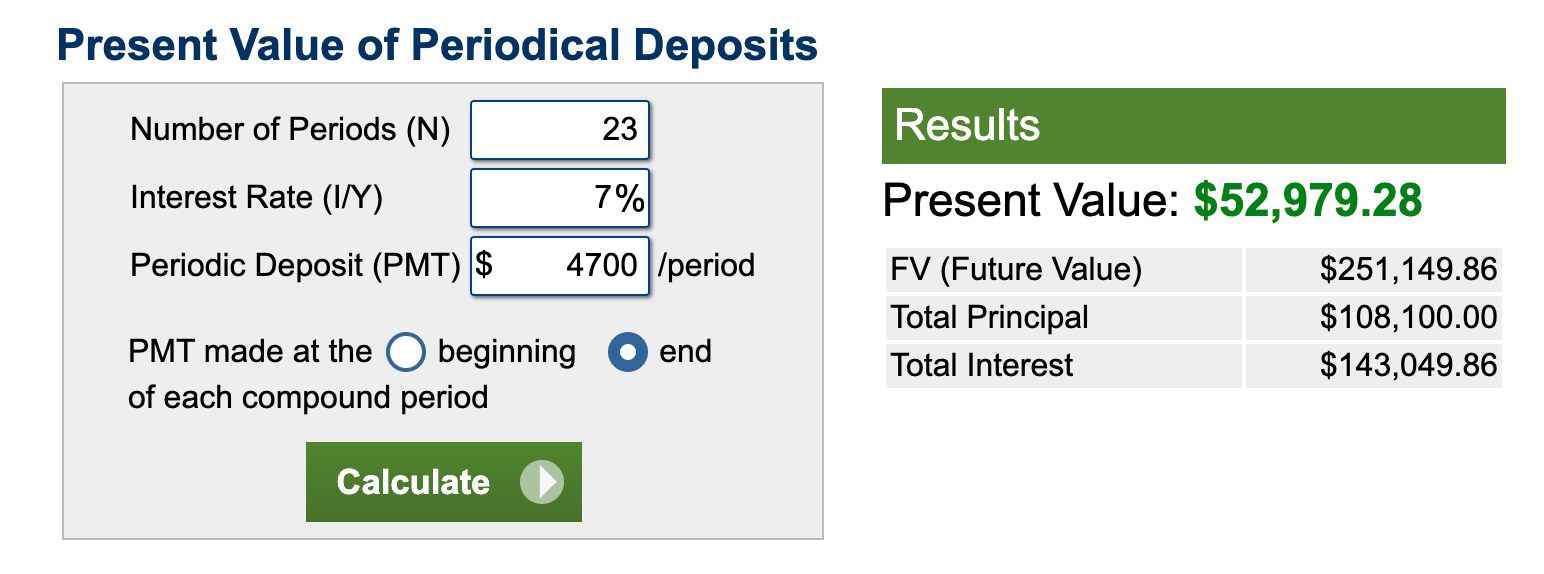
At $4,700 per year, the Future Value is $251,000. That’s about $390 per month that you’d need to invest starting today.

Do you see why this is helpful, but in a limited way?

It’s good to know that setting aside $52,000 today will give you $250,000 by the time your fake kid reaches college age, but there are a lot of assumptions being made – most obviously, the cost of college tuition 23 years from now. Hell, in 23 years from now, college might be a free online thing.

…or it could continue growing to the point that only the richest of the rich can afford it and we’ll all get plunged into illiterate serfdom where machines do everything for us and we melt in amorphous couch blobs who just watch Rick and Morty reruns in perpetuity. We honestly just don’t know. Things change, and they change rapidly.

The good news is that investing $390 per month for the next 23 years isn’t ultimately that bad or unreasonable.

Let’s do the house example

Because it’s always easier for me to do this shit in first-person, let’s figure this out as if I’m the person buying the house.

Today, my total net worth is around $160,000. About $80,000 is tied up in retirement accounts, while the other $80,000 is hanging out in taxable investment accounts or cash.

I could use that $80,000 for a down payment on a home right now, but that would represent about 50% of my net worth, and the “FI rule” about down payments is that you don’t want them to exceed 30% of your total net worth. (Illustratively, if you wanted to put $80,000 down on a $400,000 home, or 20%, that would mean your net worth would be around $270,000 to do this comfortably and sensibly. Don’t get mad at me – it’s a rule of thumb!)

How would I buy a home from now in 5 years?

Let’s say I want to plan to buy a home in 5 years from now, when I’m 31.

If I want to buy a house that costs $500,000, the 20% down payment would be $100,000. I’m already wincing, but where I live in Dallas, $500,000 will buy you a single-story two-bedroom home.

And because I don’t want to drain my principal balance in my taxable investing account that I’m planning to use first in early retirement, let’s assume that I want this $100,000 to represent an entirely separate amount of growth from what I’ve got now. In other words, I don’t want my $80,000 that I have now to count toward my $100,000. I’m starting from scratch (which is helpful for this example, in case you’re starting from scratch, too!).

In order to have $100,000 in five years from now without using my current principal balance in my taxable investing account, I’d have to invest about $17,000 per year toward my house goal in order for it to be worth $100,000 at the end of the five-year period.

So this is where the idea of opportunity cost comes in.

In my current FI plan, I’m planning to put anywhere between $2,500 and $6,000 per month into my taxable investment account to retire at 35. That’s between $30,000 and $72,000 per year. (It ranges because of my work outside of full-time employment, which fluctuates.)

If I now have to account for this house situation, that means I’m yanking $17,000 away from my early retirement taxable account, which will delay my early retirement (unless I can make more money).

Let’s flesh this out, shall we?

Now, on the lower end of the spectrum, instead of $30,000 per year toward early retirement, I’m only putting $13,000 per year toward early retirement (over the next 5 years).

The other $17,000 will go toward this $100,000 down payment.

Monthly, this means $1,083 goes into my taxable investment account and $1,416 into the house investment account, assuming $2,500 is still the amount I can afford to invest (theoretically, though, you could just be putting them into the same pot and then use $100,000 at age 30… but for the sake of this example, let’s keep them separate so the opportunity cost is obvious).

I ran the numbers on my General Investing account that I’m counting on in early retirement (the one that I mentioned is currently getting $2,500 per month, and would be knocked down to $1,083 per month for five years as I save for my hypothetical down payment), and it turns out the lower contributions for 5 years would delay my early retirement by about 2.5 years. I’ll be honest, I don’t think that’s that big of a deal (especially when you’re talking retiring at 35 or 37).

The real kicker in this situation isn’t the down payment, but instead the monthly payment.

If your rent right now is the same as what your new mortgage/insurance/taxes would be, then don’t worry about this. But if you’re like me and you’ve swung cheap rent, you have to account for the fact that your monthly payment will go up.

Right now, I pay $900/mo. in rent to split my 2BR.

Using the Zillow mortgage calculator to learn more about how much my $400,000 mortgage will set me back each month, my estimated monthly payment (mortgage, insurance, taxes) is about $2,300. If you’d like to check this for your own projection, you can use the same calculator here.

Now, assuming I’m paying for this all on my own, this is about to thunderf*** my projections. Hopefully, I’d be splitting this monthly cost with another person (read: spouse), and I’d be looking at my housing cost increasing from $900/mo. to $1,150/mo. That would mean I’d need to account for a $250 increase in my monthly expenses: $250 per month * 12 months in a year * 25 to get to FI = an additional $75,000 that would need to be saved to account for that $250 increase in my housing cost.

I’d need to save an additional $75,000 to retire (assuming my nameless spouse or renter is splitting that mortgage payment with me).

It would probably take about another year to add another $75,000 to my investment balances, so we’ll say overall the purchase of this house sets back the early retirement timeline 3 years, at a minimum.

That’s not terrible, but of course, owning a house is just generally more expensive and involves more costs (repairing your roof, hot water heaters breaking, garbage disposals on the fritz… you’ve gotta pay for it out of pocket – no more leasing agent to your rescue), so if I were a homeowner and had a mortgage and potential repairs hanging over my head, I’d probably try to save aggressively for another year on top of that to give myself cash cushion in case the roof caves in from a tornado or the foundation falls apart (#TexasProblems).

How can you apply this to your own situation?

The calculator will be your best friend if you struggled through high school precalculus the way I did, and then it just becomes dividing and conquering. For example:

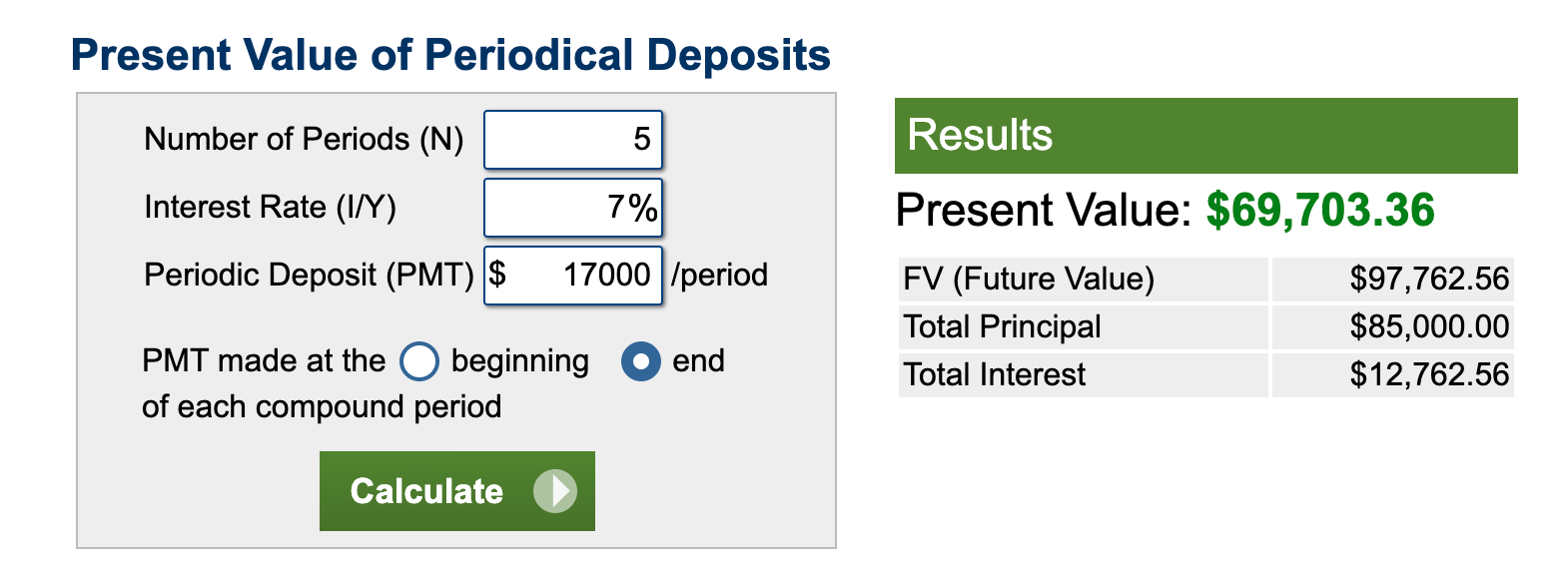
Number of periods (N) = number of years. In our example, we’re taking 5 years. 7% is our assumed interest. Periodic deposit means the amount you’ll be contributing annually. Over on the right, you’ll see FV (Future Value) as the number to pay attention to: $97,762. I’m rounding up for easy math.

I just played around with inputting different numbers into the periodic deposit and found that $17,000 per year got it close to a $100,000 future value. $18,000 per year was $103,000, so realistically, you should shoot for $17,500. You can do this same easy trial-and-erroring.

From there, you merely divide by 12 to figure out how much per month you need to be stocking away for your future purchase. Of course, if that’s too much (let’s say you don’t make enough money to invest $17,000 per year for a home), you can always extend the timeline. Maybe you wait 7 years instead.

If you extend your number of periods from 5 years to 7, you only need to invest $11,500 per year (less than $1,000 per month) to have $100,000 in 7 years.

The actual applied usefulness of this formula

I think this formula is helpful for things that have a more predictable future value – which means the timeline is probably going to be most accurate within 10 years. Once you’re talking the cost of college education 25 years away, you’re basically taking a stab in the dark.

Opportunity cost is the other big consideration. Honestly, before I wrote this post, I didn’t realize that I’d only be delaying my early retirement by a few years in order to put 20% on a half-a-million-dollar house. I’m fine with working for a few more years if it means I get to live in a bigger space that I own, but I’m certainly in no rush. In an early retirement scenario, the ideal case is to own the home outright by the time you retire so you don’t have any housing cost outside of taxes and insurance, but paying for a house in cash really has “opportunity cost” consequences. It’s worth fleshing out both timelines to see where you end up ahead.

If you’ve made it this far, congratulations. I appreciate your commitment. This stuff isn’t an exact science, but it’s fun to string together the logic and different online calculators to get rough estimates for what you’ll need to shoot for.